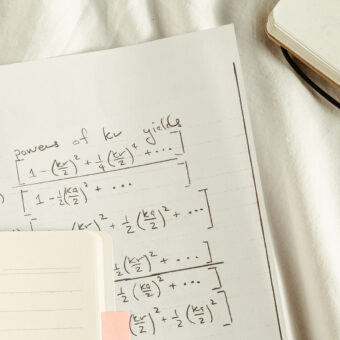Why modeling implanted metals correctly is important?
When metal implants are present in the body, they can alter the current flow during electrical stimulation, which in turn affects the electric field magnitude and distribution. This can raise safety concerns and impact the accuracy of the models used to predict the electric field distribution for dosimetric purposes. In fact, subjects with implanted metals are often excluded from transcranial electrical stimulation (tES) studies due to these concerns.
In tES the electric field distribution in the brain is estimated using patient-specific models solved with the finite element method. Therefore, accurate modeling of metal implants, if they are present, is crucial for an accurate estimation of the electric field distribution.
Implanted metals: conductors or insulators?
Metals have nominal electrical conductivity values that are several orders of magnitude higher than those of biological tissues. Thus, it may seem straightforward to model them as highly conductive or even as perfect conductors. However, this is not always the case, as we showed in a recent article titled “Modeling implanted metals in electrical stimulation applications” published in the Journal of Neural Engineering. This is because while currents in the body are ionic in nature, metals only allow for electron transport. Thus, charge transfer between biological tissues and metals requires electrochemical reactions to happen at the interface. These reactions require energy, which is provided by the voltage difference at the interface. Therefore, implanted metals may act as insulators or conductors depending on this voltage, hence on the electric field.
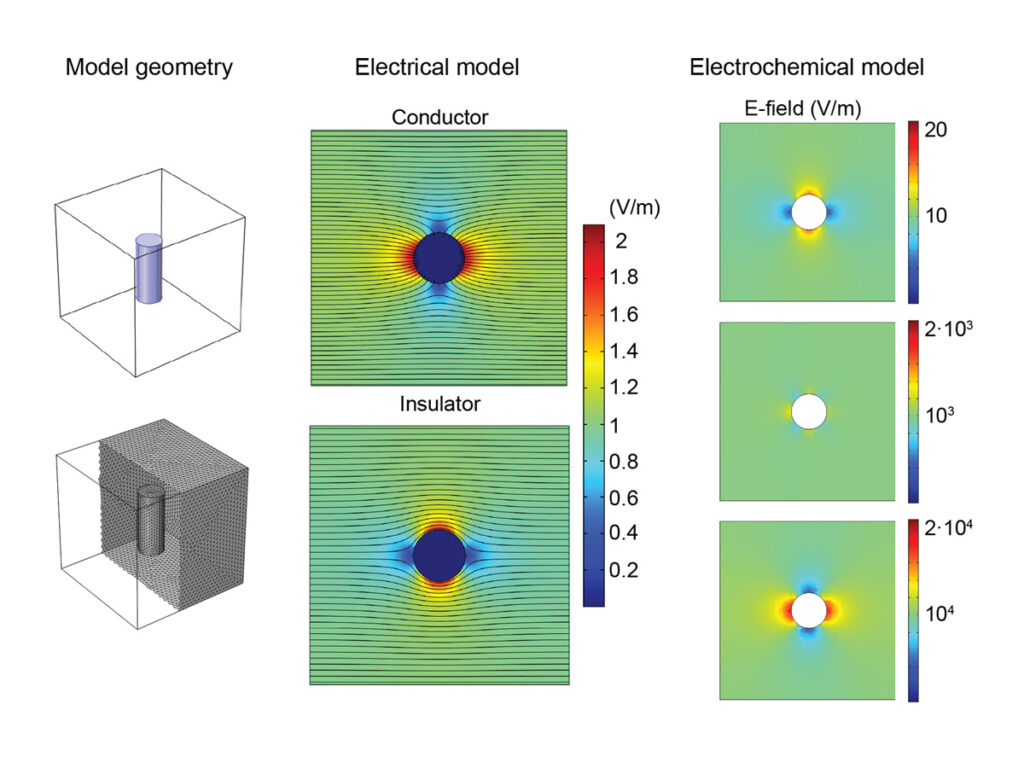
Let’s illustrate this with a simple example presented in Figure 1. The figure shows various models of a cylinder under a homogeneous electric field and how it distorts the current flow. If we model the cylinder as a perfect conductor, the field lines tend to collapse at its surface (the electric field is always perpendicular to the surface of a perfect conductor), causing a local increase in the field magnitude near the surface regions that are perpendicular to the field and a local decrease near the surface regions that are parallel to it. In contrast, if we model the cylinder as a perfect insulator, the electric field lines pass around the surface circling it (the electric field is always tangential at the surface of a perfect insulator). This causes the opposite effect: a decrease near the surface regions perpendicular to the field and an increase near the regions parallel to it.
Interestingly, if we generate the same plots using an electrochemical model, the field is distorted differently depending on the magnitude of the electric field. For low fields, the distribution resembles that obtained when modeling the implant as an insulator. On the other extreme, for large fields, the distribution is analogous to that obtained for a perfect conductor. Finally, between these two extremes, there is a range of fields where a mixed pattern is found.
Modeling choice and its impact in the estimation of the induced fields
Using models like the ones in the previous figure, in our article we showed that metal implants generally act as electric insulators for fields up to around 100 V/m, and they only resemble a perfect conductor for fields in the order of 1000 V/m and above. This behavior is independent of the implant’s metal but depends on its geometry. Furthermore, we also showed that a wrong modeling choice for implanted metals can lead to errors of 50% or more in the estimation of the induced fields. Therefore, accurately representing the behavior of metal implants in numerical simulations is crucial for assessing the dosimetry of electrical stimulation techniques.